Il problema del lampione

 

SCHEDA DOCENTE

 

 

Questa scheda ha la funzione di guidare il docente esplicitando i passaggi logici da me previsti per la fase II dello svolgimento del compito.

 

Per prima cosa si sottolineerà agli studenti che il problema richiede l’illuminazione in maniera uniforme del parco. Se il problema invece avesse richiesto, per esempio, che i tre vertici fossero illuminati con uguale intensità il problema sarebbe stato presto risolto posizionando il lampione nel circocentro. Inoltre, se il problema avesse richiesto che il lampione venisse posizionato a distanza uguale dai tre lati del parco il problema sarebbe stato subito risolto posizionando il lampione nell’incentro del triangolo.

Posto invece che il problema richiede un’illuminazione uniforme del parco è necessario fare alcune riflessioni.

Nel discutere i risultati ottenuti dai quattro gruppi relativi ai quattro centri notevoli del triangolo ho previsto che il docente faccia costruire, con Geogebra, ad ogni gruppo un unico triangolo e i suoi quattro centri
notevoli facendo corrispondere ad ogni centro uno strumento di Geogebra appositamente costruito.
Analizzerà quindi, insieme alla classe (mostrando per esempio la figura tramite un video proiettore), i vari casi al variare del tipo di triangolo e della forma. Si può fare notare anche che il circocentro, il baricentro e l’ortocentro sono sempre allineati per qualunque triangolo. La retta che li congiunge si chiama retta di Eulero. (file di Geogebra da scaricare)

 

Partendo dal caso più semplice (il triangolo equilatero) si evidenzierà quindi la coincidenza di circocentro, incentro, baricentro e ortocentro e si parlerà delle proprietà di simmetria della figura. La conclusione in questo caso sarà quindi che esiste un centro di simmetria e questo è indifferentemente uno dei quattro punti notevoli del triangolo. Questo è ovviamente il caso più semplice ed evidente su dove verrebbe piazzato il lampione per illuminare in maniera più uniforme possibile il parco. In questo caso il centro di simmetria è equidistante dai vertici e dai punti medi dei lati. La figura sarà come quella di seguito mostrata.

 

 

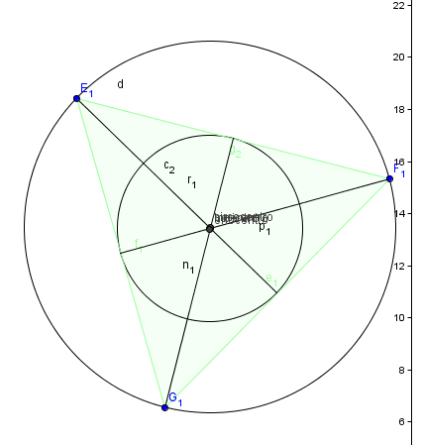
Si passerà poi ad analizzare il caso del triangolo isoscele. In questo caso i quattro centri notevoli sono allineati. L’ortocentro è in posizione molto periferica come anche l’incentro. Stessa sorte tocca al circocentro se si continua ad allontanare verso sinistra il vertice E1 poiché aumenta il raggio della circonferenza circoscritta. Anche ad occhio il punto più adatto alla scopo sembra essere il baricentro.

 

 

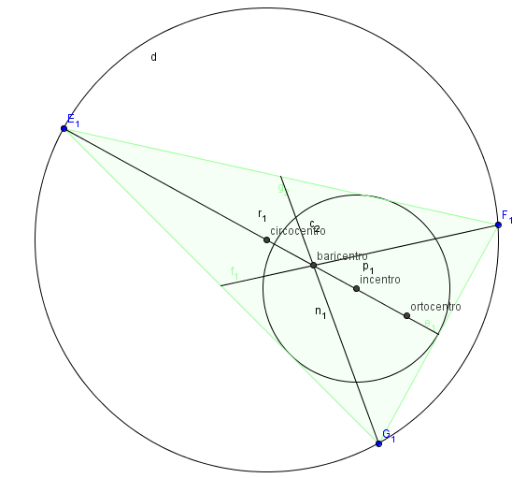
Considerando poi il caso di un triangolo scaleno bisogna distinguere i casi di triangolo ottusangolo e triangolo acutangolo.

 

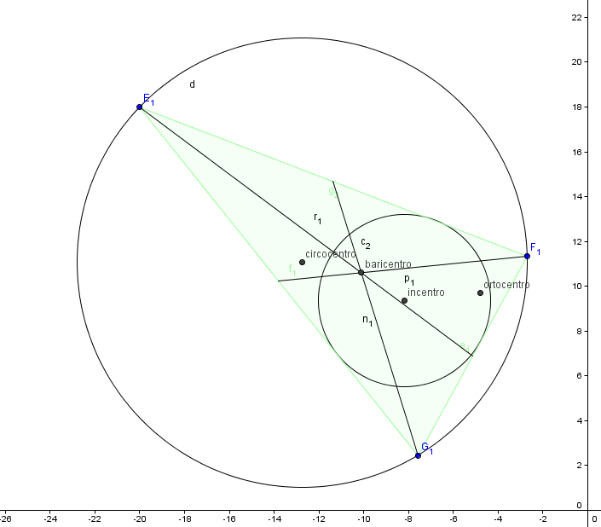
Per il triangolo ottusangolo si vede subito che circocentro e ortocentro cadono fuori dal triangolo (possono essere anche molto distanti a seconda della figura e questo sarebbe un inutile spreco di energia elettrica!). Invece incentro e baricentro sono interni anche se, in questo caso, è da preferire il baricentro per la sua posizione meno periferica rispetto l’incentro il quale darebbe luogo ad una illuminazione sicuramente poco uniforme essendo molto lontano da E1.

 

 

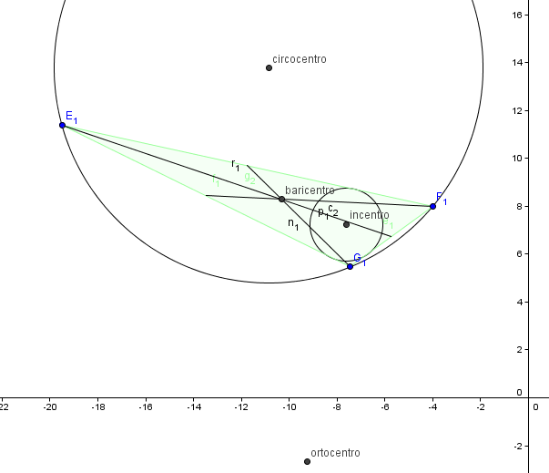
L’ultimo è il caso del triangolo scaleno acutangolo. In questo caso i quattro centri notevoli del triangolo sono tutti interni. L’ortocentro è molto periferico e anche il circocentro. Anche in questo caso sembra proprio il baricentro il punto migliore se vogliamo l’illuminazione più uniforme possibile.

 

Si possono a questo punto fare delle considerazioni sulle proprietà del baricentro, in particolare quella di avere per coordinate i valori medi delle coordinate dei tre vertici.

 

La conclusione generale dovrebbe quindi essere quella che se lo scopo è quello di illuminare in modo più uniforme possibile il parco allora la scelta più appropriata è quella del baricentro indipendentemente dalla forma particolare del parco triangolare.

 

 

 

 

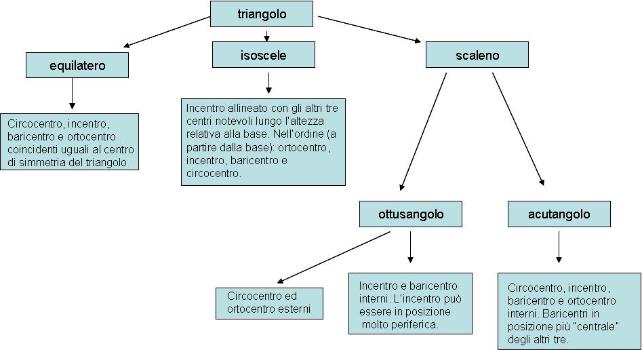
Allo scopo di riassumere tutto il docente costruirà una mappa come quella mostrata nella figura seguente.